Dijkstra’s Algorithm in C [With Code]

Here you will learn about Dijkstra’s algorithm and how you can implement it in C programming.

Dijkstra algorithm is also called the single source shortest path algorithm. It is based on the greedy technique. The algorithm maintains a list visited[ ] of vertices, whose shortest distance from the source is already known.

If visited[1], equals 1, then the shortest distance of vertex i is already known. Initially, visited[i] is marked as, for source vertex.

At each step, we mark visited[v] as 1. Vertex v is a vertex at the shortest distance from the source vertex. At each step of the algorithm, the shortest distance of each vertex is stored in an array distance[ ].

Also Read: Prim’s Algorithm in C

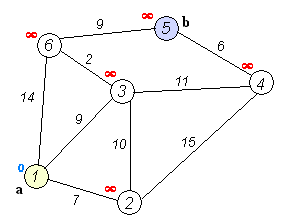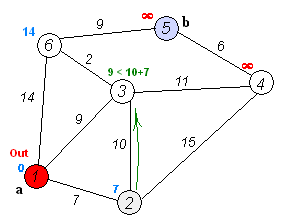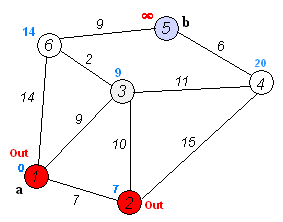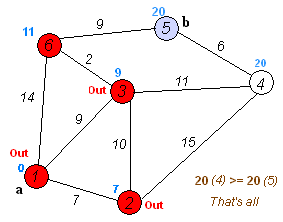
Dijkstra’s Algorithm

1. Create cost matrix C[ ][ ] from adjacency matrix adj[ ][ ]. C[i][j] is the cost of going from vertex i to vertex j. If there is no edge between vertices i and j then C[i][j] is infinity.

2. Array visited[ ] is initialized to zero.

               for(i=0;i<n;i++)

                              visited[i]=0;

3. If the vertex 0 is the source vertex then visited[0] is marked as 1.

4. Create the distance matrix, by storing the cost of vertices from vertex no. 0 to n-1 from the source vertex 0.

               for(i=1;i<n;i++)

                              distance[i]=cost[0][i];

Initially, the distance of the source vertex is taken as 0. i.e. distance[0]=0;

5. for(i=1;i<n;i++)

– Choose a vertex w, such that distance[w] is minimum and visited[w] is 0. Mark visited[w] as 1.

– Recalculate the shortest distance of remaining vertices from the source.

– Only, the vertices not marked as 1 in the array visited[ ] should be considered for recalculation of distance. i.e. for each vertex v

               if(visited[v]==0)

                              distance[v]=min(distance[v],

                              distance[w]+cost[w][v])

Time Complexity

The program contains two nested loops each of which has a complexity of O(n). n is the number of vertices. So the complexity of the algorithm is O(n²).

Dijkstra’s Algorithm Program in C

Here is the C Program on Dijkstra Algorithm for finding the Minimum Distance of Vertices from a Given Source in a Graph.

#include<stdio.h>
#include<conio.h>
#define INFINITY 9999
#define MAX 10

void dijkstra(int G[MAX][MAX],int n,int startnode);

int main()
{
	int G[MAX][MAX],i,j,n,u;
	printf("Enter no. of vertices:");
	scanf("%d",&n);
	printf("\nEnter the adjacency matrix:\n");
	
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			scanf("%d",&G[i][j]);
	
	printf("\nEnter the starting node:");
	scanf("%d",&u);
	dijkstra(G,n,u);
	
	return 0;
}

void dijkstra(int G[MAX][MAX],int n,int startnode)
{

	int cost[MAX][MAX],distance[MAX],pred[MAX];
	int visited[MAX],count,mindistance,nextnode,i,j;
	
	//pred[] stores the predecessor of each node
	//count gives the number of nodes seen so far
	//create the cost matrix
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			if(G[i][j]==0)
				cost[i][j]=INFINITY;
			else
				cost[i][j]=G[i][j];
	
	//initialize pred[],distance[] and visited[]
	for(i=0;i<n;i++)
	{
		distance[i]=cost[startnode][i];
		pred[i]=startnode;
		visited[i]=0;
	}
	
	distance[startnode]=0;
	visited[startnode]=1;
	count=1;
	
	while(count<n-1)
	{
		mindistance=INFINITY;
		
		//nextnode gives the node at minimum distance
		for(i=0;i<n;i++)
			if(distance[i]<mindistance&&!visited[i])
			{
				mindistance=distance[i];
				nextnode=i;
			}
			
			//check if a better path exists through nextnode			
			visited[nextnode]=1;
			for(i=0;i<n;i++)
				if(!visited[i])
					if(mindistance+cost[nextnode][i]<distance[i])
					{
						distance[i]=mindistance+cost[nextnode][i];
						pred[i]=nextnode;
					}
		count++;
	}

	//print the path and distance of each node
	for(i=0;i<n;i++)
		if(i!=startnode)
		{
			printf("\nDistance of node%d=%d",i,distance[i]);
			printf("\nPath=%d",i);
			
			j=i;
			do
			{
				j=pred[j];
				printf("<-%d",j);
			}while(j!=startnode);
	}
}

Output:

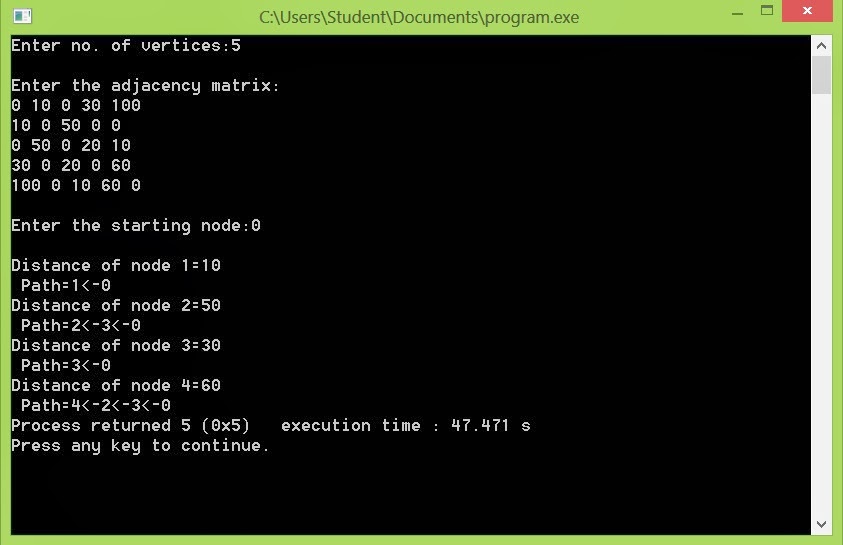
This program calculates the shortest distance from the starting node to all the other nodes in the graph. It also prints the distance and the path from the starting node to each node.

The algorithm works by maintaining a list of visited nodes. And for each unvisited node, it calculates the distance to that node from the starting node and updates the distance and the path if a shorter path is found.

The algorithm continues until all nodes have been visited, and the shortest distance and the path to each node have been calculated.

Now I hope you know how to implement this algorithm in C. Comment below if you have any queries or found something wrong in Dijkstra’s algorithm in C.